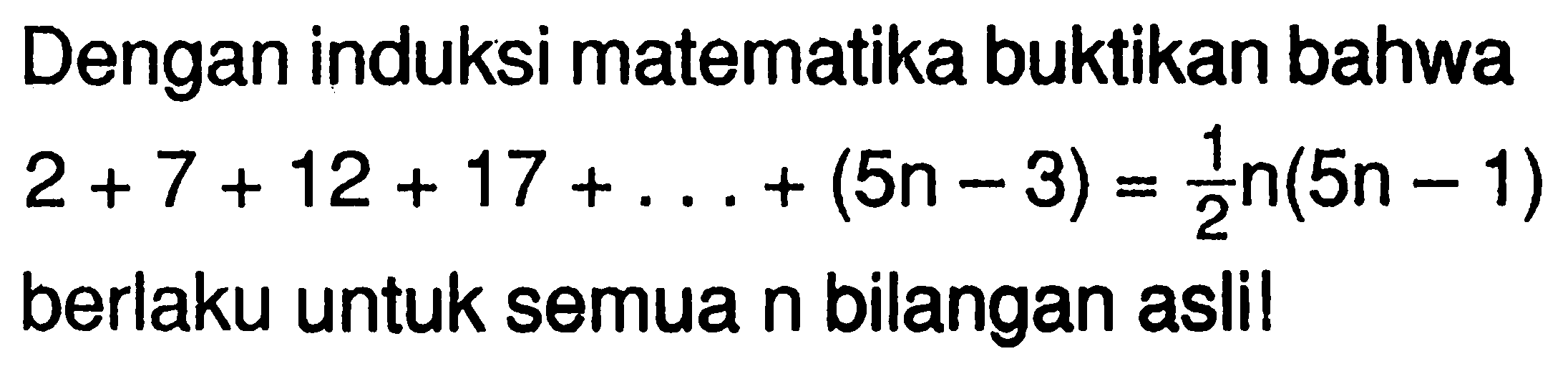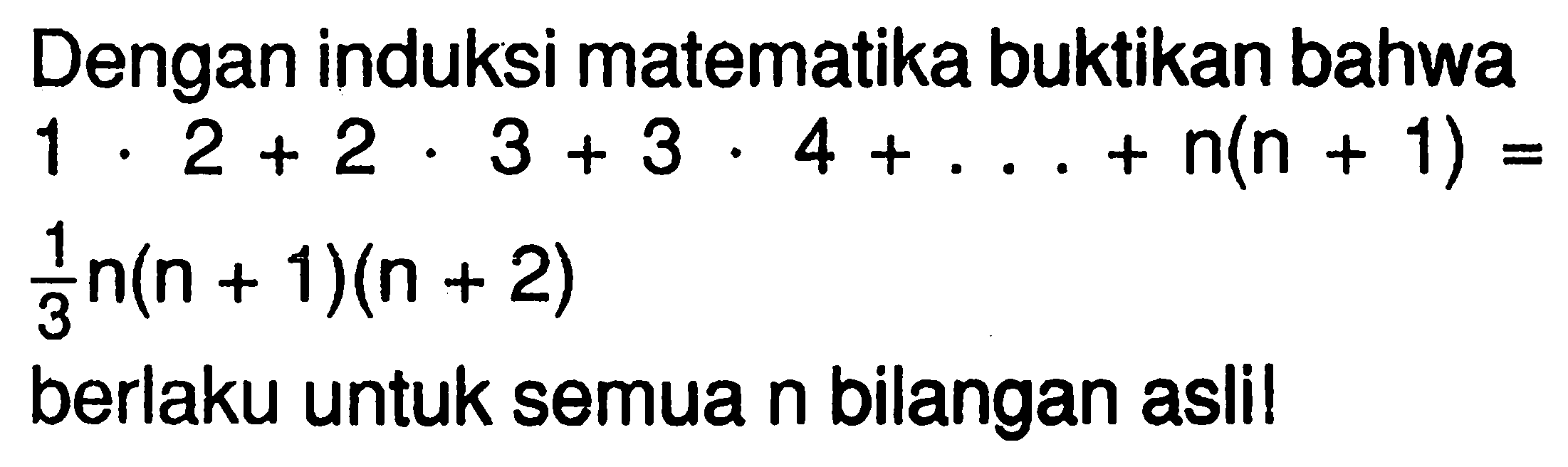Colearn Logo
  • Tanya
  • 11 SMA
  • Matematika

Video Contoh Soal Induksi Matematika Kelas 11

Dengan induksi matematika buktikan bahwa 2+7+12+17+0....+(5n-3)=1/2 n(5n-1) berlaku untuk semua n bilangan asli!
03:28

Dengan induksi matematika buktikan bahwa 2+7+12+17+0....+...

Buktikan n^3- n habis dibagi 3 untuk setiap bilangan asli n > 1.
03:49

Buktikan n^3- n habis dibagi 3 untuk setiap bilangan asli...

Buktikan dengan induksi matematika bahwa 3+6+10+15+ . . . +1/2(n+1)(n+2)=1/6 n(n^2+6n+11) berlaku untuk semua n bilangan asli.
05:25

Buktikan dengan induksi matematika bahwa 3+6+10+15+ . . ....

Buktikan pernyataan-pernyataan berikut menggunakan induksi matematika. (x-y) adalah faktor dari x^(2n)-y^(2n) untuk setiap bilangan asli n.
03:37

Buktikan pernyataan-pernyataan berikut menggunakan induks...

Misalkan diketahui barisan bilangan a1, a2, a3, ..., dengan a1=2, a2=5, a3=8, dan an=a(n-1)+a(n-2)+a(n-3). Buktikan bahwa an<=2^n.
03:30

Misalkan diketahui barisan bilangan a1, a2, a3, ..., deng...

Dengan induksi matematika untuk S(k+1), sigma i=1 n (3i-2) = (n/2)(3n-1) akan menjadi . . . .
01:11

Dengan induksi matematika untuk S(k+1), sigma i=1 n (3i-2...

Koefisien x^4 dari penjabaran (1 + 2x + 3x^2)^10 adalah
04:38

Koefisien x^4 dari penjabaran (1 + 2x + 3x^2)^10 adalah

Buktikan bahwa untuk setiap bilangan asli n, berlaku sigma i=1 n i^4=1^4+2^4+3^4+...+n^4=(n(n+1)(6n^3+9n^2+n-1))/30
09:20

Buktikan bahwa untuk setiap bilangan asli n, berlaku sigm...

Bentuk notasi sigma sigma k=8 20 (2k^2-3k+1) dengan batas bawah 1 adalah ...
01:59

Bentuk notasi sigma sigma k=8 20 (2k^2-3k+1) dengan batas...

Buktikan bahwa 6x7^n-2x3^n habis dibagi untuk setiap n bilangan asli.
03:50

Buktikan bahwa 6x7^n-2x3^n habis dibagi untuk setiap n bi...

Pertanyaan seputar CoLearn

  1. Apa yang dimaksud dengan induksi matematika?

    Induksi matematika adalah salah satu cara pembuktian suatu rumus atau pernyataan matematika dan akan menghasilkan suatu kesimpulan.

  2. Apa yang dimaksud dengan penalaran induktif dan deduktif?

    Penalaran deduktif adalah penalaran dengan menarik kesimpulan dari premis umum ke premis spesifik. Premis sendiri adalah pemikiran atau asumsi. Sedangkan penalaran induktif merupakan kebalikan dari penalaran deduktif dimana menarik kesimpulan dari premis spesifik ke premis umum.

  3. Apa saja prinsip induksi matematika?

    Prinsip induksi matematika:

    1. P(1) benar, untuk n = 1 maka P(n) adalah bernilai benar
    2. Untuk setiap bilangan asli k, jika P(k) benar maka P(k + 1) ialah juga benar

  4. Apa yang dimaksud dengan penalaran logika secara induktif?

    Pengertian penalaran logika secara induktif adalah kebalikan dari penalaran deduktif dimana kesimpulan ditarik dari premis spesifik ke premis umum.

  5. Apa rumus induksi matematika?

    1. P(1) benar, untuk n = 1 maka P(n) adalah bernilai benar
    2. Untuk setiap bilangan asli k, jika P(k) benar maka P(k + 1) ialah juga benar

Ngerti materi denganTanya

Cari soal Matematika, Fisika, Kimia dan tonton video pembahasan biar ngerti materinya.

  • Matematika, Fisika dan Kimia
  • SD (Kelas 5-6), SMP dan SMA
  • 300,000+ video pembahasan soal
  • Semua video udah dicek kebenarannya
Understand Tanya benefits

Sukses nggak pernah instan. Latihan topik lain, yuk!

© 2021 CoLearn. Hak Cipta Dilindungi.

Neco Bathing